거듭제곱의 합(sum of powers, power sum)은 크게 두 가지로 나눌 수 있다: 지수가 변하는 것과 밑이 변하는 것.
지수가 변하는 거듭제곱의 합
가장 기본적인 형태는

이다. 이를 미분하여  를 곱하면 다음을 얻는다.
를 곱하면 다음을 얻는다.

비슷한 방법으로 어떤 양의 정수  에 대하여
에 대하여

를 구할 수 있다.
급수  는
는  일 때 수렴하며
일 때 수렴하며  이다. 일반적으로
이다. 일반적으로

가 된다. 이와 비슷한 유한 합은

이다.
밑이 변하는 거듭제곱의 합
가장 기본적인 형태는

이다. 이는 위 경우에 비하여 계산하기가 어렵다. 고교 과정에서는  의 경우를 배우는데, 이항정리를 이용하여 귀납적으로 이끌어낸다.
의 경우를 배우는데, 이항정리를 이용하여 귀납적으로 이끌어낸다.  를 만들기 위하여
를 만들기 위하여  를 이용한다. 이 식을
를 이용한다. 이 식을  에서부터
에서부터  까지 더하면
까지 더하면

이다. 이를


로 정리하면 원하는 식을 얻는다.
베르누이 수를 이용하면 귀납적이지 않은 하나의 식으로 위의 합을 나타낼 수 있다. 오일러-매클로린 공식을 이용하여

에서  로 두면,
로 두면,

이 식에서 계수들의 합이 1이라는 것을 쉽게 알 수 있다.

또한 두 개의 파라미터로 변하는 급수로도 나타낼 수 있다.

공식










1부터의 연속한 자연수의 합
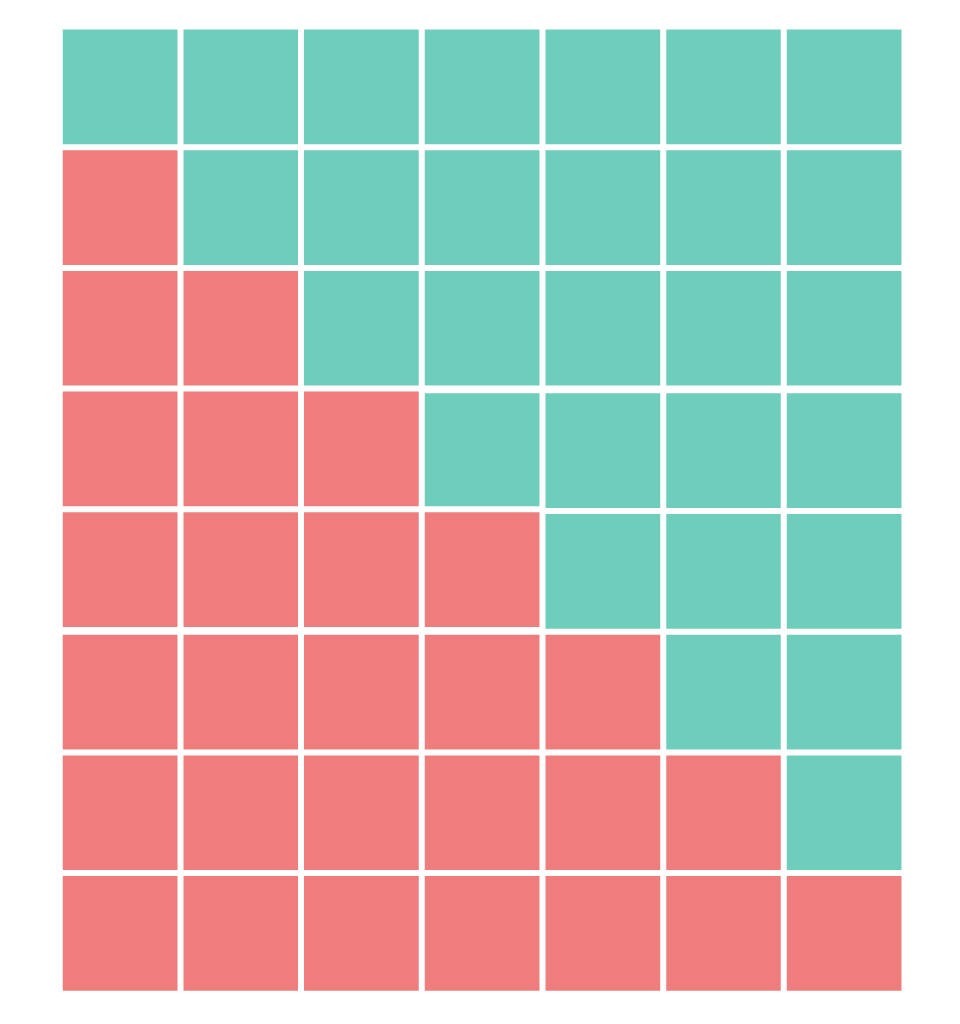 같은 색으로 표현된 도형은
같은 색으로 표현된 도형은  를 나타내고, 가로는
를 나타내고, 가로는  , 세로는
, 세로는  임에서 공식을 유도할 수 있다.
임에서 공식을 유도할 수 있다.
특히 연속한 자연수의 합은 여러 가지 방법으로 구할 수 있다. 가장 알기 쉬운 방법으로는, 소문으로 들려오는 가우스가 어렸을 때 썼다는 방법이 있다.
|
1 |
+ |
2 |
+ |
… |
+ |
(n-1) |
+ |
n
|
| +) |
n |
+ |
(n-1) |
+ |
… |
+ |
2 |
+ |
1
|
|
|
|
(n+1) |
+ |
(n+1) |
+ |
… |
+ |
(n+1) |
+ |
(n+1) |
 개 개
|
위에서  임을 알 수 있다.
임을 알 수 있다.
니코마코스의 정리
 가로와 세로가 모두
가로와 세로가 모두  이고, 한 변의 길이가
이고, 한 변의 길이가  인 정사각형이
인 정사각형이  개 있으므로 그 넓이의 합은
개 있으므로 그 넓이의 합은  이고 공식이 유도된다.
이고 공식이 유도된다.
세제곱의 합 공식

을 보면, 누구나 자연수의 합 공식의 제곱으로 나타남을 알 수 있을 것이다.

이를 니코마코스의 정리(Nicomachus's theorem)라고 한다.
참고











































