거듭제곱의 합 (sum of powers, power sum)은 크게 두 가지로 나눌 수 있다: 지수가 변하는 것과 밑이 변하는 것.
지수가 변하는 거듭제곱의 합 가장 기본적인 형태는
∑
i
=
0
n
x
i
=
x
n
+
1
−
1
x
−
1
{\displaystyle \sum _{i=0}^{n}x^{i}={\frac {x^{n+1}-1}{x-1}}}
이다. 이를 미분하여
x
{\displaystyle x}
∑
i
=
0
n
i
x
i
=
x
−
(
n
+
1
)
x
n
+
1
+
n
x
n
+
2
(
x
−
1
)
2
.
{\displaystyle \sum _{i=0}^{n}ix^{i}={\frac {x-(n+1)x^{n+1}+nx^{n+2}}{(x-1)^{2}}}.}
비슷한 방법으로 어떤 양의 정수
e
i
(
i
=
0
,
⋯
,
m
)
{\displaystyle e_{i}\quad (i=0,\cdots ,m)}
∑
k
=
m
n
k
e
0
(
k
−
1
)
e
1
⋯
(
k
−
m
)
e
m
x
k
{\displaystyle \sum _{k=m}^{n}k^{e_{0}}(k-1)^{e_{1}}\cdots (k-m)^{e_{m}}x^{k}}
를 구할 수 있다.
급수
∑
k
≥
0
x
k
{\displaystyle \sum _{k\geq 0}x^{k}}
|
x
|
<
1
{\displaystyle |x|<1}
∑
k
≥
0
x
k
=
(
1
−
x
)
−
1
{\displaystyle \sum _{k\geq 0}x^{k}=(1-x)^{-1}}
(
∑
k
≥
0
x
k
)
p
=
(
1
−
x
)
−
p
=
∑
n
≥
0
(
n
+
p
−
1
n
)
x
n
{\displaystyle \left(\sum _{k\geq 0}x^{k}\right)^{p}=(1-x)^{-p}=\sum _{n\geq 0}{\binom {n+p-1}{n}}x^{n}}
가 된다. 이와 비슷한 유한 합은
(
∑
k
=
0
n
x
k
)
p
=
1
(
p
−
1
)
!
∑
k
=
0
n
p
(
n
−
|
n
−
k
|
+
p
−
1
)
!
n
−
|
n
−
k
|
!
x
k
{\displaystyle \left(\sum _{k=0}^{n}x^{k}\right)^{p}={\frac {1}{(p-1)!}}\sum _{k=0}^{np}{\frac {(n-|n-k|+p-1)!}{n-|n-k|!}}x^{k}}
이다.
밑이 변하는 거듭제곱의 합 가장 기본적인 형태는
∑
i
=
0
n
i
p
{\displaystyle \sum _{i=0}^{n}i^{p}}
이다. 이는 위 경우에 비하여 계산하기가 어렵다. 고교 과정에서는
p
=
1
,
2
,
3
{\displaystyle p=1,2,3}
이항정리 를 이용하여 귀납적 으로 이끌어낸다.
∑
i
=
0
n
i
p
{\displaystyle \sum _{i=0}^{n}i^{p}}
(
x
+
1
)
p
+
1
−
x
p
+
1
=
∑
j
=
0
p
(
p
+
1
j
)
x
j
{\displaystyle (x+1)^{p+1}-x^{p+1}=\sum _{j=0}^{p}{\binom {p+1}{j}}x^{j}}
i
=
0
{\displaystyle i=0}
i
=
n
{\displaystyle i=n}
∑
i
=
0
n
(
(
i
+
1
)
p
+
1
−
i
p
+
1
)
=
(
n
+
1
)
p
+
1
=
∑
i
=
0
n
∑
j
=
0
p
(
p
+
1
j
)
i
j
=
∑
j
=
0
p
(
p
+
1
j
)
∑
i
=
0
n
i
j
{\displaystyle \sum _{i=0}^{n}\left((i+1)^{p+1}-i^{p+1}\right)=(n+1)^{p+1}=\sum _{i=0}^{n}\sum _{j=0}^{p}{\binom {p+1}{j}}i^{j}=\sum _{j=0}^{p}{\binom {p+1}{j}}\sum _{i=0}^{n}i^{j}}
이다. 이를
(
n
+
1
)
p
+
1
−
∑
j
=
0
p
−
1
(
p
+
1
j
)
∑
i
=
0
n
i
j
=
(
p
+
1
p
)
∑
i
=
0
n
i
p
{\displaystyle (n+1)^{p+1}-\sum _{j=0}^{p-1}{\binom {p+1}{j}}\sum _{i=0}^{n}i^{j}={\binom {p+1}{p}}\sum _{i=0}^{n}i^{p}}
∑
i
=
0
n
i
p
=
(
n
+
1
)
p
+
1
p
+
1
−
1
p
+
1
∑
j
=
0
p
−
1
(
p
+
1
j
)
∑
i
=
0
n
i
j
{\displaystyle \sum _{i=0}^{n}i^{p}={\frac {(n+1)^{p+1}}{p+1}}-{\frac {1}{p+1}}\sum _{j=0}^{p-1}{\binom {p+1}{j}}\sum _{i=0}^{n}i^{j}}
로 정리하면 원하는 식을 얻는다.
베르누이 수 를 이용하면 귀납적이지 않은 하나의 식으로 위의 합을 나타낼 수 있다. 오일러-매클로린 공식 을 이용하여
∑
k
=
1
n
f
(
k
)
=
∫
1
n
f
(
x
)
d
x
+
1
2
(
f
(
1
)
+
f
(
n
)
)
+
∑
k
=
1
∞
B
k
k
!
(
f
(
k
−
1
)
(
b
)
−
f
(
k
−
1
)
(
a
)
)
{\displaystyle \sum _{k=1}^{n}f(k)=\int _{1}^{n}f(x)\mathrm {d} x+{\frac {1}{2}}(f(1)+f(n))+\sum _{k=1}^{\infty }{\frac {B_{k}}{k!}}\left(f^{(k-1)}(b)-f^{(k-1)}(a)\right)}
에서
f
(
k
)
=
k
p
{\displaystyle f(k)=k^{p}}
∑
k
=
1
n
k
p
=
n
p
+
∑
k
=
0
p
B
k
p
!
k
!
(
p
−
k
+
1
)
!
n
p
−
k
+
1
=
∑
k
=
1
p
+
1
(
−
1
)
p
−
k
+
1
B
p
−
k
+
1
p
!
k
!
(
p
−
k
+
1
)
!
n
k
{\displaystyle \sum _{k=1}^{n}k^{p}=n^{p}+\sum _{k=0}^{p}{\frac {B_{k}p!}{k!(p-k+1)!}}n^{p-k+1}=\sum _{k=1}^{p+1}{\frac {(-1)^{p-k+1}B_{p-k+1}p!}{k!(p-k+1)!}}n^{k}}
이 식에서 계수들의 합이 1이라는 것을 쉽게 알 수 있다.
∑
k
=
1
p
+
1
(
−
1
)
p
−
k
+
1
B
p
−
k
+
1
p
!
k
!
(
p
−
k
+
1
)
!
=
1
{\displaystyle \sum _{k=1}^{p+1}{\frac {(-1)^{p-k+1}B_{p-k+1}p!}{k!(p-k+1)!}}=1}
또한 두 개의 파라미터로 변하는 급수로도 나타낼 수 있다.
∑
i
=
0
n
k
p
=
∑
i
=
1
p
∑
j
=
0
i
−
1
(
−
1
)
j
(
i
−
j
)
p
(
n
+
p
−
i
+
1
n
−
i
)
(
p
+
1
j
)
{\displaystyle \sum _{i=0}^{n}k^{p}=\sum _{i=1}^{p}\sum _{j=0}^{i-1}(-1)^{j}(i-j)^{p}{\binom {n+p-i+1}{n-i}}{\binom {p+1}{j}}}
공식
∑
k
=
0
n
k
=
1
2
n
(
n
+
1
)
{\displaystyle \sum _{k=0}^{n}k={\frac {1}{2}}n(n+1)}
∑
k
=
0
n
k
2
=
1
6
n
(
n
+
1
)
(
2
n
+
1
)
{\displaystyle \sum _{k=0}^{n}k^{2}={\frac {1}{6}}n(n+1)(2n+1)}
∑
k
=
0
n
k
3
=
1
4
n
2
(
n
+
1
)
2
{\displaystyle \sum _{k=0}^{n}k^{3}={\frac {1}{4}}n^{2}(n+1)^{2}}
∑
k
=
0
n
k
4
=
1
30
n
(
n
+
1
)
(
2
n
+
1
)
(
3
n
2
+
3
n
−
1
)
{\displaystyle \sum _{k=0}^{n}k^{4}={\frac {1}{30}}n(n+1)(2n+1)(3n^{2}+3n-1)}
∑
k
=
0
n
k
5
=
1
12
n
2
(
n
+
1
)
2
(
2
n
2
+
2
n
−
1
)
{\displaystyle \sum _{k=0}^{n}k^{5}={\frac {1}{12}}n^{2}(n+1)^{2}(2n^{2}+2n-1)}
∑
k
=
0
n
k
6
=
1
42
n
(
n
+
1
)
(
2
n
+
1
)
(
3
n
4
+
6
n
3
−
3
n
+
1
)
{\displaystyle \sum _{k=0}^{n}k^{6}={\frac {1}{42}}n(n+1)(2n+1)(3n^{4}+6n^{3}-3n+1)}
∑
k
=
0
n
k
7
=
1
24
n
2
(
n
+
1
)
2
(
3
n
4
+
6
n
3
−
n
2
−
4
n
+
2
)
{\displaystyle \sum _{k=0}^{n}k^{7}={\frac {1}{24}}n^{2}(n+1)^{2}(3n^{4}+6n^{3}-n^{2}-4n+2)}
∑
k
=
0
n
k
8
=
1
90
n
(
n
+
1
)
(
2
n
+
1
)
(
5
n
6
+
15
n
5
+
5
n
4
−
15
n
3
−
n
2
+
9
n
−
3
)
{\displaystyle \sum _{k=0}^{n}k^{8}={\frac {1}{90}}n(n+1)(2n+1)(5n^{6}+15n^{5}+5n^{4}-15n^{3}-n^{2}+9n-3)}
∑
k
=
0
n
k
9
=
1
20
n
2
(
n
+
1
)
2
(
n
2
+
n
−
1
)
(
2
n
4
+
4
n
3
−
n
2
−
3
n
+
3
)
{\displaystyle \sum _{k=0}^{n}k^{9}={\frac {1}{20}}n^{2}(n+1)^{2}(n^{2}+n-1)(2n^{4}+4n^{3}-n^{2}-3n+3)}
∑
k
=
0
n
k
10
=
1
66
n
(
n
+
1
)
(
2
n
+
1
)
(
n
2
+
n
−
1
)
(
3
n
6
+
9
n
5
+
2
n
4
−
11
n
3
+
3
n
2
+
10
n
−
5
)
{\displaystyle \sum _{k=0}^{n}k^{10}={\frac {1}{66}}n(n+1)(2n+1)(n^{2}+n-1)(3n^{6}+9n^{5}+2n^{4}-11n^{3}+3n^{2}+10n-5)}
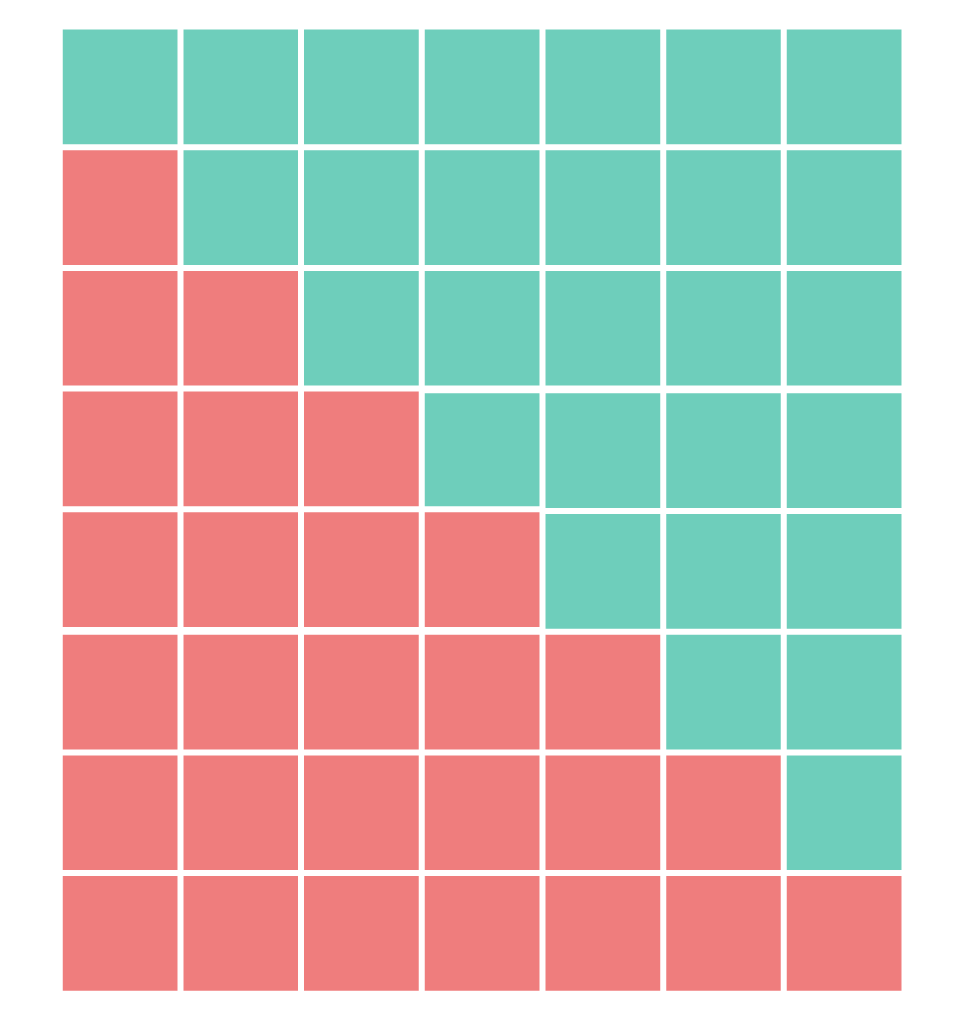
1부터의 연속한 자연수의 합 같은 색으로 표현된 도형은
∑
k
=
1
n
k
{\displaystyle \sum _{k=1}^{n}k}
n
{\displaystyle n}
n
+
1
{\displaystyle n+1}
특히 연속한 자연수의 합은 여러 가지 방법으로 구할 수 있다. 가장 알기 쉬운 방법으로는, 소문으로 들려오는 가우스 가 어렸을 때 썼다는 방법이 있다.
1
+
2
+
…
+
(n-1)
+
n
+)
n
+
(n-1)
+
…
+
2
+
1
(n+1)
+
(n+1)
+
…
+
(n+1)
+
(n+1)
n
{\displaystyle \quad n}
위에서
2
∑
k
=
1
n
k
=
n
(
n
+
1
)
,
∑
k
=
1
n
k
=
1
2
n
(
n
+
1
)
{\displaystyle 2\sum _{k=1}^{n}k=n(n+1),\quad \sum _{k=1}^{n}k={\frac {1}{2}}n(n+1)}
니코마코스의 정리 가로와 세로가 모두
∑
k
=
1
n
k
{\displaystyle \sum _{k=1}^{n}k}
k
{\displaystyle k}
k
{\displaystyle k}
k
2
⋅
k
=
k
3
{\displaystyle k^{2}\cdot k=k^{3}}
세제곱의 합 공식
∑
k
=
1
n
k
3
=
1
4
n
2
(
n
+
1
)
2
{\displaystyle \sum _{k=1}^{n}k^{3}={\frac {1}{4}}n^{2}(n+1)^{2}}
을 보면, 누구나 자연수의 합 공식의 제곱으로 나타남을 알 수 있을 것이다.
∑
k
=
1
n
k
3
=
(
∑
k
=
1
n
k
)
2
{\displaystyle \sum _{k=1}^{n}k^{3}=\left(\sum _{k=1}^{n}k\right)^{2}}
이를 니코마코스의 정리 (Nicomachus's theorem)라고 한다.
참고